Kelas : X IPS 3
Absen : 22
Sistem Persamaan Kuadrat-Kuadrat (SPKK)
Sistem persamaan kuadrat-kuadrat (SPKK) adalah sistem persamaan yang terdiri atas dua persamaan kuadrat yang masing-masing memuat dua variabel. SPKK memiliki beberapa macam bentuk, tetapi dalam artikel ini kita akan lebih banyak membahas bentuk yang paling sederhana, yaitu kedua persamaan kuadrat berbentuk eksplisit. Bentuk umumnya adalah sebagai berikut.
y = ax2 + bx + c ……………. (bagian kuadrat pertama) |
y = px2 + qx + r ……………. (bagian kuadrat kedua) |
Dengan a, b, c, p, q, dan r merupakan bilangan-bilangan real.
Secara umum, untuk memperoleh penyelesaian SPKK dilakukan langkah-langkah sebagai berikut.
Langkah 1:
Subtitusikan bagian kuadrat persamaan pertama ke bagian kuadrat yang kedua atau sebaliknya sehingga diperoleh persamaan kuadrat baru.
Langkah 2:
Selesaikan persamaan kuadrat baru yang diperoleh pada langkah pertama.
Langkah 3:
Subtitusikan nilai x yang diperoleh pada langkah kedua ke persamaan pertama atau persamaan kedua. Untuk mempermudah perhitungan, silahkan kalian pilih persamaan kuadrat yang lebih sederhana.
Contoh Soal 1:
Tentukan himpunan penyelesaian SPKK berikut dan gambarkan sketsa grafik tafsiran geometrinya.
y = x2
y = 2x2 – 3x
Jawab:
Subtitusikan bagian kuadrat yang pertama y = x2 ke bagian kuadrat yang kedua y = 2x2 – 3x sehingga diperoleh:
⇒ x2 = 2x2
⇒ 2x2 – x2 – 3x = 0
⇒ x2 – 3x = 0
⇒ x(x – 3) = 0
⇒ x = 0 atau x = 3
Selanjutnya, subtitusikan nilai x = 0 dan x = 3 ke bagian kuadrat yang pertama y = x2.
■ Untuk x = 0 diperoleh:
⇒ y = x2
⇒ y = (0)2
⇒ y = 0
■ Untuk x = 3 diperoleh:
⇒ y = x2
⇒ y = (3)2
⇒ y = 9
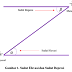
Dengan demikian, himpunan penyelesaian SPKK itu adalah {(0, 0), (3, 9)}. Anggota-anggota dari himpunan penyelesaian SPKK tersebut secara geometris dapat ditafsirkan sebagai koordinat titik potong antara parabola y = x2 dengan parabola y = 2x2 – 3x. Untuk lebih jelasnya, perhatikan gambar di bawah ini.
Contoh Soal 2:
Tentukan himpunan penyelesaian SPKK berikut dan gambarkan sketsa grafik tafsiran geometrinya.
y = x2 – 1
y = x2 – 2x – 3
Jawab:
Subtitusikan bagian kuadrat yang pertama y = x2 – 1 ke bagian kuadrat yang kedua y = x2 – 2x – 3 sehingga diperoleh:
⇒ x2 – 1 = x2 – 2x – 3
⇒ x2 – x2 = –2x – 3 + 1
⇒ 2x = –2
⇒ x = –1
Selanjutnya, subtitusikan nilai x = –1 ke persamaan y = x2 – 1 sehingga diperoleh:
⇒ y = x2 – 1
⇒ y = (–1)2 – 1
⇒ y = 1 – 1
⇒ y = 0
Dengan demikian, himpunan penyelesaian dari SPKK tersebut adalah {(–1, 0)}. Tafsiran geometrinya adalah grafik parabola y = x2 – 1 dan parabola y = x2 – 2x – 3 berpotongan di satu titik, yaitu di (–1, 0). Perhatikan gambar di bawah ini.